The study question

Properly articulating the research question can help with critical decision making, including determining whether the question posed can be answered with a cross-sectional design, or whether there is even need to collect primary data (e.g. comparable secondary data sources already exist). Furthermore, it can help with developing appropriate survey instruments that have relevant content and coherent flow. To reduce measurement bias, new survey questions should undergo cognitive testing. Previously validated survey instruments could also be adapted for new information collection activities.

Sometimes, a survey is multi-purpose, with several primary outcomes of interest (and possibly different target populations)¹⁴. As a general principle, only the minimum amount of data needed should be collected, and no identifying/potentially identifying information should be assessed, except unless it is absolutely critical to the research question. Direct identifiers include any information collected that provides a reasonable basis to identify an individual; examples of such direct identifies include the following 18 categories: name; all geographical subdivisions smaller than state (street, city, county, zip codes or equivalent geocodes, except for initial 3 digits of a zip code); all elements of dates, except year; all ages >89 years (unless aggregated into single category of age >90 years); telephone and fax number; email, IP address, URL; social security number/passport number; medical record number; health plan beneficiary number; account number; certificate license number; vehicle identification number, device identifiers, and serial number; full face photographs, biometric identifiers; and any other unique identifying number, characteristic or code^15,16. Institute Review Board approval should be sought when direct identifiers or potentially identifying information might be needed or possibly collected; at all times, adequate access controls should be implemented to safeguard protected records (Table 1).

The target population of the survey

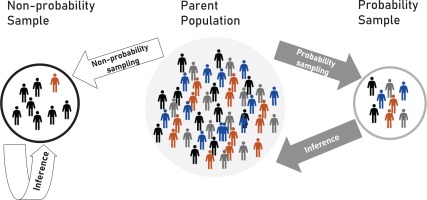
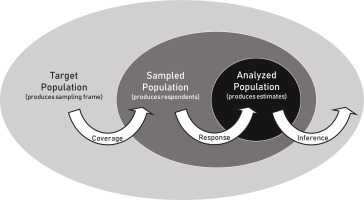
Failure to properly define the target population from which the sample is being drawn could create challenges with making inferences from the sample back to the target population (Figure 1). The target population is determined by the purpose for which data are being collected. In public health, data collection activities are generally classified as either research or public health practice, based on intent to create generalizable knowledge^17,18. Research activities (e.g. population surveys) have an intent to generalize findings from the studied population to the larger target population (Figure 2). In contrast, activities deemed as public health practice (e.g. focus groups) have no intent to generalize findings beyond the immediate participants studied; the studied population therefore is the same as the target population.

Figure 1

The cycle of inference for non-probability versus probability based samples

Figure 2

Algorithm for decision making in relation to sampling approach in survey design

In research activities, the target population could be defined on the basis of different factors, including geographical (e.g. a county), population (e.g. children), administrative (e.g. program directors), occupational/vocational (e.g. employees or students), or facilities (e.g. clinics). It could also be defined by an event (e.g. birth, death, diagnoses, survivorship, immigration, or emigration), or a behavior (e.g. current tobacco use). Regardless of the criterion used, the epidemiological concepts of person, place, and time should be used to frame the target population. The presence of several target populations within the same survey might have implications for questionnaire design (skip patterns) and sample size calculations (minimum sample size needed).

Survey population

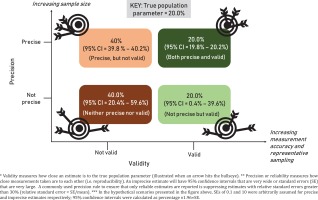
This item touches on issues of precision; a large sample is more precise than a smaller sample (Figure 3). The fundamental approach to sample size calculation does not differ between web versus traditional survey modes; however, more stringent assumptions may be needed for web surveys (e.g. smaller anticipated response rate). Questions which investigators might grapple with during sample size calculations include: ‘How do I ensure that I can generate reliable estimates for the smallest-sized subgroups of interest in my study?’; ‘What if I have several outcomes or target populations within the same survey?’; ‘How do I determine reasonable estimates of the different parameters needed for sample size calculation?’.

Figure 3

Four hypothetical scenarios demonstrating differences in validity* and precision** using an arbitrarily chosen population parameter (i.e. ‘gold standard’) of 20% for prevalence of an unspecified outcome***

The following principles are applied when performing sample size calculations:

Sample size calculation is not needed if one performs a complete census of all individuals listed in the sampling frame. The decision to do a census rather than take a sample can be considered in light of the low response rates typical of web surveys, and also given the fact that the incremental cost of recruiting or contacting an additional participant in a web survey is negligible. When a complete census is taken rather than a sample, there are no associated sampling errors, and hence confidence intervals are not warranted when reporting point estimates (confidence intervals are similarly not scientifically justifiable for non-probability samples because there are no sampling errors either).

Sampling or selecting the participants in a representative manner

This item deals with issues of validity; a probability based sample (e.g. simple random sample) is more valid than a non-probability based sample (e.g. convenience sample). A non-probability sample is so named because selection probabilities are unknown and cannot be numerically calculated for each eligible individual¹⁴. The underlying basis for probability, i.e. randomization, is absent in non-probability samples; people opt in or opt out willfully and deliberately (e.g. volunteer samples where individuals self-select into the study, convenience samples where remote or inaccessible units are deliberately ignored by the investigators, or snowball sampling where existing participants recruit new participants from their own network). Selection probabilities could therefore be zero for certain eligible individuals in a non-probability sample. With probability based samples on the other hand, selection involves randomization; selection probabilities are therefore known, non-zero, and numerically calculable for everyone in the study since both the numerator (respondents) and the denominator (all those eligible) are well defined, positive integers.

While a plethora of non-probability web-based data collection activities exist and do have their role in public health practice (e.g. focus groups, semi-structured interviews, volunteer survey panels)^19-21, probability based sampling is central to inferential surveillance activities. Any one of the numerous approaches to probabilistic sampling (Figures 1 and 2) will theoretically yield valid estimates in the absence of coverage and non-response biases. If a simple random or systematic sampling will be conducted within the context of a web survey, an important first step is to construct a sampling frame — a list of all the sampling units in the study universe, from which the sample will be drawn. Efforts should be made to ensure that the sampling frame is current, correct, and complete.

Sending the survey invitations in a manner that is efficient, safe, and mitigates bias

Sending large-volume survey invitations en bloc via regular email is likely to get flagged as suspicious or malicious activity and blocked by anti-virus software, internet service providers, or corporate mail administrators²². In particular, the use of the ‘To’ ‘Cc’ or ‘Bcc’ features of emails to invite multiple individuals within the same email should be discouraged as this might lead to unfavorable response rates because of being perceived as spam, or triggering ripple unsubscribe requests. Investigators could use a program with features that allow for batch mailing, customizing delivery to each recipient (e.g. ‘Dear John Q. Public’ instead of ‘Dear participant’), and tracking those who have not responded (to send targeted reminders). Several commercial and open access programs exist for data collection with varying capabilities, including RED Cap (Research Electronic Data Capture; https://www.project-redcap.org/); Epi Info Web Survey (https://www.cdc.gov/epiinfo/cloud.html); Survey Monkey (https://www.surveymonkey.com/); and Google forms (https://www.google.com/forms/about/). A determination of in which environment to host data collection should include a careful consideration of data volume (i.e. total number of respondents), variety (e.g. text-only vs photo/video illustrated questions), vulnerability (e.g. sensitive information and direct identifiers), cost, as well as the software’s capabilities (e.g. security controls, ability to implement skip patterns and to filter respondents and non-respondents). Survey administrators should pre-test the survey application on different devices (e.g. computers, smartphones, and tablets) and using different browsers/browser settings to ensure optimal display across different platforms. Skip patterns, when used, should appear seamless with no apparent discontinuation in the ordering of question numbers from the survey taker’s perspective to reduce potential for confusion; alternatively, the entire questionnaire could be unnumbered.

Whenever possible, customized links should be provided for each participant to ensure that each email invitation can only be completed once and by the intended recipient. When only a generic link exists where anyone who has the link can access the survey, recipients should be discouraged from forwarding the survey to any other person. If individuals not in the sampling frame were to be forwarded the survey and complete it, the probability based attributes of the survey begin to get eroded and the survey begins to assume characteristics of a snowball (non-probability) sample.

The consent process could be administered in the introduction page of the web survey; it should be clear to participants that proceeding with the survey indicates that they understand the purpose of the study and agree to participate. The survey team’s contact information should also be provided in the introduction page for participants to send questions or concerns about the survey. Completed responses from study participants should be fully delinked from their email or cell phone numbers. Where direct or potential identifiers are being collected, all responses completed online should be done in a secure, electronic, web-based data collection system hosted within an infrastructure where the survey administrators have full control of the data. The survey should have an opening and closing date, after which responses will no longer be recorded. After the survey closing date, data should be transferred from the Server database into a flat database and stored on secured, password protected computers where they will be accessible only to the investigators.

When financial incentives are being used to increase response rates, care should be exercised in the amount offered so that no selection bias is introduced inadvertently (e.g. differential participation rates by individuals of low and high socioeconomic status). Consideration should also be given to the timing of web survey launches and follow-up reminders to ensure optimal response rates. For example, inviting academic faculty or students to complete a web survey during periods of peak school activity (e.g. exam periods) might yield low response rates.

Assessing and enhancing the external validity of collected data

Two threats to external validity or generalizability in a web survey are poor coverage and low response rates (Figure 4). Poor coverage occurs when the sampling frame does not cover the entire target population. When significant coverage bias exists, a mixed mode survey could be implemented to increase the extent of coverage; for example, a traditional survey mode (e.g. telephone, postal mail, or face-to-face surveys) could be added to the web mode to ensure that everybody in the target population has a known, and non-zero probability of selection. Alternatively, the study population could be redefined (narrowed) such that the areas of non-coverage are excluded.

Figure 4

Relationships between the target, sampled, and analyzed populations in a survey

Testing for non-response bias is especially important in web surveys because of the typically high rates of non-response. A validation survey which involves conducting a follow-up survey on a sample of non-respondents, would typically be needed to empirically test differences between respondents and non-respondents. Intensive efforts are often needed to elicit a response from original non-respondents within validation surveys, including use of incentives, using a shortened version of the questionnaire to encourage response, and using additional ways to contact participants, beyond merely emailing, e.g. direct mail, phone calls or in-person visit. Besides helping to detect non-response, a validation survey can help mitigate non-response bias, while also increasing the effective response rate. Several scientific journals will only publish findings from surveys with ‘high’ response rates, as such there is a strong motivation to increase the effective response rate of low-response web surveys.

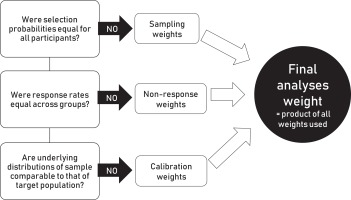
Where necessary, different types of weights, including sampling weights (inverse of selection probabilities), non-response weights (inverse of the response rate), and calibration weights (standardizing the demographic distributions of the sample to that of the parent population) may be used to enhance the external validity of a survey (Figure 5). All, none or a variable number of these weights may be applied depending on sampling approach used, patterns of non-response observed, and the availability of data on sampling frame characteristics. For example, sampling weights only apply when selection probabilities are differential (e.g. oversampling of certain groups); they do not apply when selection probabilities are equal for everyone (e.g. simple random, or systematic sampling). Similarly, non-response weights only apply when non-response rates are differential across groups (i.e. not when all groups have comparably high or comparably low response rates). Calibration weights can only be created when data are available on the demographic distribution of the parent population. The final analysis weight is computed as the product of the individual weights used.

Figure 5

Anatomy of survey weights used to adjust for differential selection probabilities and response rates, and to calibrate the sample to the standard population